Overview
Working on a recent project, I needed to use red-black trees for tracking data. However, the last time I ever looked at red-black trees was as a first-year undergraduate more than twenty years ago. And even then, we did not implement them — I vaguely recall a lone lecture, a quiz, and then on to the next algorithm. So it was none too surprising that when I started googling around, there were lots of questions to be found about balanced trees, few answers, and almost no valid implementations to be found (or none at all, depending on the flavor of balanced tree). It would appear that detailed experimentation with balanced trees is unusual in most undergrad programs.
Diagrams, rough outlines, and incomplete pseudocode are one thing, but working code is something completely different. Especially when that code needs to be used in an embedded system and must therefore be free from external dependencies (to say nothing of freedom from the pollution of open source licences).
To up the challenge more, most sources only go into detail about inserting data
into a balance tree (and often leave symmetric cases as exercises for the
reader
), then handwave the subject of deletion.
So I dug out my stack of undergrad and graduate textbooks, googled around for more information, then implemented a few variations of 2-3 trees and red-black trees — after all, a red-black tree is really a 2-3 three that has been shoehorned into a binary tree, with a semantically meaningless color applied to each node.
In this short series of articles, I'm going to cover two different versions of 2-3 trees, and two versions of red-black trees. Since a red-black tree is just a 2-3 tree in a color-confused dress, I'll start with two-three trees and work up from there. If nothing else, I'm writing these up to convince myself I finally understand how they work.
Working source code and a test app can be found in balanced_tree.zip.
Note: If you're looking for a working implementation of 2-3 trees, do not use this code. This version of 2-3 trees does work, but it is inefficient. Use the version described in Interior 2-3 Trees. This implementation is for given solely for informational purposes.
Exterior 2-3 Trees
The implementation I'm going to cover in this article is based on the algorithm described in Aho, Hopcroft, and Ullman, Data Structures and Algorithms. In the 1987 reprint (hey, it was new when I got it), this is described on pages 169-180. Like most such references, they have moderately detailed pseudocode for insertion, but only very sketchy (to reuse Aho et al.'s word) pseudocode for deletion.
For want of a better name, I'm calling this an exterior
2-3 tree, since all data
values are stored at the leaves. On the one hand, I think this is the simplest
implementation to cover (if nothing else, it was the easiest place for me to start).
At the same time, the restriction of only storing data in the leaf nodes makes it
the least memory efficient (and cache usage is a major performance factor on modern
computers) and the slowest (all operations are O(log n) time).
A 2-3 tree is a form of balanced tree, with two important properties:
- All interior nodes have either two or three children.
- Every path from the root to a leaf has exactly the same length.
The only exception to this is for a tree with only one leaf, which needs to be handled as a special case.
The way a 2-3 tree maintains these properties is that no operation can
insert or delete a subtree. Insertions are done in one of two ways:
splitting a subtree or moving a subtree from one sibling to another (AKA
rebalancing
). Similarly, a deletion will either merge sibling
nodes or move a subtree from one sibling to another.
The critical point is that the depth of the tree can only change in one place: the root of the tree. Once the tree ends up in a state where all nodes along a path contain 3 children, inserting a new child under that subtree will require splitting the root of the tree. This is accomplished by inserting a new root node and making the previous root (which is now split into 2 siblings) the child of the new root.
To put it another way, splitting and merging can never change the depth of a node within the tree (except, of course, for the root node). Splits and merges can only change the width of the tree (the number of nodes at a particular level). A node will never move up or down the tree as a result of either a split or a merge, they may only move sideways.
The same is true for deletion: If every node along a path contains only 2 children, deleting a child will require successively merging parents all the way up to the root. Because the root has no sibling, it cannot be merged; therefore the old root will be deleted, making its only child the new root.
Because it is not possible to change the depth of any sub-tree, the depth of every leaf in the tree stays at a constant depth. That depth can only change due to mergering or splitting the root of the tree.
Since all data values are stored in the leaves with this type of tree, every look-up, insertion, and deletion operation must traverse down to a leaf (even if the value to look up or delete is not in the tree). Therefore every operation on the tree has a Little-O, Big-O, and Big-Omega time of log n. That means this implementation is algorithmically the slowest of the balanced tree algorithms being covered in these articles.
Data Structures
For evaluation purposes, I define a simple key-value pair, where data is
sorted with an unsigned 32-bit integer. The value is a blind
void* pointer. This pointer is not used for testing, it is
simply the value returned when doing a look-up operation in the resulting
binary tree.
struct VoidRef_t
{
U32 Key;
void* pContext;
};
Each node in the tree uses the following structure:
struct TwoThreeExterior_t
{
TwoThreeExterior_t *pChild1;
TwoThreeExterior_t *pChild2;
TwoThreeExterior_t *pChild3;
VoidRef_t Ref;
U32 Low1;
U32 Low2;
U32 Low3;
bool IsLeaf;
};
Each interior node of the tree will have either 2 or 3 children (hence the
reason it is called a 2-3 Tree
). A leaf node will always have all three
child pointers set to NULL.
In addition, each interior node must keep track of the lowest key stored
under each child node. This allows the code to determine which child node
might contain a search key (e.g., for Low1 <= x < Low2,
the key will be found in the first child).
A boolean is used to mark leaf nodes, although this is done mostly to keep
the code easier to read and to allow for self-consistency tests. Every leaf
node will have NULL == pChild1, therefore replacing the boolean
with a test for NULL would improve performance by reducing the
memory footprint of each node. However, since this is almost the slowest
implementation I tested (second only to left leaning red-black trees), there
is little point in attempting to optimize it.
One difference in this code from the Aho version of 2-3 trees is that Aho only caches the low key for the second and third children of each node. While this is adequate for searches, it causes problems when balancing the tree. Since child pointers may be shuffled left or right within a node, or moved into a sibling node, keeping a cached copy of the first child's lowest key eliminates the need to traverse to the leftmost leaf when merging or splitting nodes.
Insertion
Most of the logic required for insertion is fully recursive. Special case handling is required for the root to handle insertion into an empty tree, or when an insertion requires the root to be split.
For this implementation, all of the recursive code is contained in
InsertRec(). Because all of the data values are stored in
the leaves, the code must first recurse all the way down to a leaf.
Once the value is inserted (which may not occur if the key is already
in the tree), the code will recurse back out, rebalancing the tree on
the way, and updating the cached low values.
InsertRec() returns a pointer to the node that was updated.
Initially this is a pointer to the newly inserted node. After reaching
the bottom level of recursion, this pointer tracks nodes that where split.
The reason for this is that the code needs access to the parent of the node
in order to propertly insert the split node back into the tree. Once no
further splits are required, InsertRec() will return NULL,
and the only further work required is to update the cached low keys.
Note that one difference between this code and Aho is that their version
tracks the smallest key of pNew and returns it. Their approach
is mildly cumbersome (and more an artifact of the Pascal-like format of their
pseudocode), and requires passing more data around. Due to the logic of
insertion, after a recursive call the low keys that are cached in
pChild will be correct, so we can directly reference
pNode's children to update its lows and keep
everything in sync.
TwoThreeExterior_t*
TwoThreeExterior::InsertRec(TwoThreeExterior_t *pNode, VoidRef_t ref)
{
TwoThreeExterior_t *pNew = NULL;
// The first half of this function is dedicated to descending down the
// tree until it reaches the leaf node where the insertion should occur.
//
if (false == pNode->IsLeaf) {
//
// Determine which of the 2 or 3 children should contain the element
// that is being inserted.
//
U32 childIndex = Child_3;
TwoThreeExterior_t *pChild = pNode->pChild3;
if (ref.Key < pNode->Low2) {
childIndex = Child_1;
pChild = pNode->pChild1;
}
else if ((NULL == pNode->pChild3) || (ref.Key < pNode->Low3)) {
childIndex = Child_2;
pChild = pNode->pChild2;
}
// Recurse down the appropriate child.
TwoThreeExterior_t *pBack = InsertRec(pChild, ref);
// If a non-NULL pointer was returned, we need to insert it into
// pNode, which may require splitting pNode.
if (NULL != pBack) {
// If pNode only contains two children, we can insert pBack
// into pNode without requiring a split.
//
// Note that due to the logic of InsertRec(), pBack should be
// the second child of pNode since it is guaranteed to contain a
// key larger than pChild. The recursive call to InsertRec()
// will swap the contents of pBack and pChild to guarantee that
// this is true.
//
if (NULL == pNode->pChild3) {
pNode->IsLeaf = false;
// If the insertion was to the second child, we can drop
// pBack in as the third child without any extra effort.
if (Child_2 == childIndex) {
pNode->pChild3 = pBack;
pNode->Low3 = pBack->Low1;
}
// However, if the insertion was to the first child, pBack
// needs to be inserted after it -- again making it the
// second child. This requires shifting the current second
// child over to be the third child, then dropping pBack in
// as the third child.
else {
pNode->pChild3 = pNode->pChild2;
pNode->Low3 = pNode->pChild2->Low1;
pNode->pChild2 = pBack;
pNode->Low2 = pBack->Low1;
// Note that we must fix up the cached low key for the
// first child, since the recursive call may have swapped
// the contents of pChild and pBack before returning,
// meaning that pNode's cached key is now invalid.
pNode->Low1 = pNode->pChild1->Low1;
}
}
// Otherwise pNode is a 3-node, so we need to split it into a
// pair of 2-nodes.
else {
pNew = NewNode();
pNew->IsLeaf = false;
// pBack is to the right of child 3, so child 3 and pBack
// become the children of the new node.
if (Child_3 == childIndex) {
pNew->pChild1 = pNode->pChild3;
pNew->Low1 = pNode->pChild3->Low1;
pNew->pChild2 = pBack;
pNew->Low2 = pBack->Low1;
}
// pBack comes between child 2 and child 3, so pBack and
// child 3 become the children of pNew -- the difference
// from the previous condition being the order in which
// they are stored in pNew
else if (Child_2 == childIndex) {
pNew->pChild1 = pBack;
pNew->Low1 = pBack->Low1;
pNew->pChild2 = pNode->pChild3;
pNew->Low2 = pNode->pChild3->Low1;
}
// Otherwise pBack comes between child 1 and child 2, so
// we have to move child 2 and child 3 into pNew, then
// make pBack the second child of pNode
else {
pNew->pChild1 = pNode->pChild2;
pNew->Low1 = pNode->pChild2->Low1;
pNew->pChild2 = pNode->pChild3;
pNew->Low2 = pNode->pChild3->Low1;
pNode->pChild2 = pBack;
pNode->Low2 = pBack->Low1;
// Again, the recursive call to InsertRec() may have
// swapped pChild and pBack before returning, so we
// have to fix up the cached low key for child 1.
pNode->Low1 = pNode->pChild1->Low1;
}
pNode->pChild3 = NULL;
pNode->Low3 = 0;
}
}
// Otherwise the child node was changed, but pNode does not need to
// be split after the insert. However, we still need to update the
// correct low key for the node to guarantee that it is being
// cached correctly.
//
else if (Child_1 == childIndex) {
pNode->Low1 = pNode->pChild1->Low1;
}
else if (Child_2 == childIndex) {
pNode->Low2 = pNode->pChild2->Low1;
}
else {
pNode->Low3 = pNode->pChild3->Low1;
}
}
// Once the code hits a leaf, this block of code will create a new node
// to contain the data (or return NULL if nothing was inserted).
else {
// Leaf nodes should never be empty unless we're dealing with a
// degenerate tree (possibly resulting from deleting all elements,
// then attempting to insert a new element).
//
// But we do need to detect and prevent a key from being inserted
// into the tree multiple times -- this implementation of 2-3 trees
// does not support duplicate keys.
//
if ((NULL != pNode->Ref.pContext) && (ref.Key != pNode->Ref.Key)) {
pNew = NewNode();
// Arrange pNode and pNew so that pNode contains the smaller of
// the two keys. We'll return pNew so that the caller can
// insert the new node into the parent (or split the parent if
// necessary).
if (pNode->Ref.Key < ref.Key) {
pNew->Ref = ref;
pNew->Low1 = ref.Key;
}
else {
pNew->Ref = pNode->Ref;
pNew->Low1 = pNode->Ref.Key;
pNode->Ref = ref;
pNode->Low1 = ref.Key;
}
}
// Special case for when the leaf node has nothing in it.
// This is needed for inserting into a tree that contains a
// single, empty node -- in practice, this should never happen.
//
// Otherwise, this condition will handle replacing the old value
// when the key is already in the tree: no allocation is required,
// just overwrite the old value.
//
else {
pNode->Ref = ref;
pNode->Low1 = ref.Key;
// NOTE: This leaves pNew set to NULL, so the caller knows that
// nothing needs to be updated.
}
}
// If a new node was created, we need to pass it to the caller so it can
// add it to the parent node (possibly requiring the parent to be split).
return pNew;
}
The top-level Insert() function handles the special cases for
insertion: insertion into an empty tree, and splitting the root node.
void TwoThreeExterior::Insert(VoidRef_t ref)
{
// In the normal case, the tree is not empty.
if (NULL != m_pRoot) {
// Normally all of the insertion work will be done recursively by
// InsertRec(). However, insertion may cause nodes to be split,
// which can propagate up the tree to the root.
//
// If this returns a non-NULL pointer, then the current root has
// been split, and pBack is a sibling for the current root.
//
TwoThreeExterior_t *pBack = InsertRec(m_pRoot, ref);
// Create a new root, with m_pRoot and pBack as its children.
//
// InsertRec() will have swapped the contents of the current m_pRoot
// with pNode to assure that m_pRoot < pNode. Therefore this
// code can safely make m_pRoot the first child and pNode the second
// child of the new root node.
//
// Note that this increases the depth of the tree by one.
//
if (NULL != pBack) {
TwoThreeExterior_t *pNew = NewNode();
pNew->IsLeaf = false;
pNew->pChild1 = m_pRoot;
pNew->pChild2 = pBack;
pNew->Low1 = m_pRoot->Low1;
pNew->Low2 = pBack->Low1;
m_pRoot = pNew;
}
}
// Special case for inserting into an empty tree.
else {
m_pRoot = NewNode();
m_pRoot->IsLeaf = true;
m_pRoot->Ref = ref;
m_pRoot->Low1 = ref.Key;
}
}
By way of example, take the following 2-3 tree:
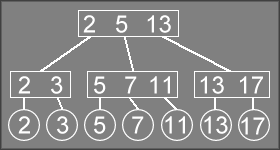
For the purposes of these diagrams, rectangles are internal nodes and circles are external (leaf) nodes.
To insert the value 9
into the tree, we call Insert which
will recurse down to the leaf node where it should insert the 9
. This
will produce a call stack similar to this:
Insert("9")InsertRec("2 5 13", "9")InsertRec("5 7 11", "9")InsertRec("7", "9")
At the bottom level of recursion, InsertRec will call
NewNode to create a node, in which it will store the 9
.
It then returns the new node containing 9
.
Upon stepping back one level of recursion, we have a node containing
5 7 11
with an extra 9
. Conceptually, this should produce a 4-node
containing 5 7 9 11
.
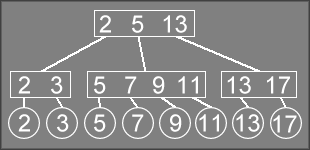
However, since we cannot have a node containing 4 values, we change the
node so it contains 5 7
and create a new node that will contain 9 11
.
This new node is then returned from InsertRec, so after
stepping back one more level of recursion, we conceptually have a 4-node
containing 2 5 9 13
.
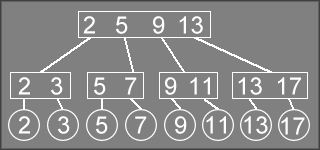
This is also an invalid state, so we change this node node to contain
2 5
, and create a new node that contains 9 13
, which is returned
from this call to InsertRec.
At this point, we are back to the main Insert function.
When Insert gets a non-NULL pointer from
InsertRec it will split the root of the tree, creating
a new root that contains 2 9
.
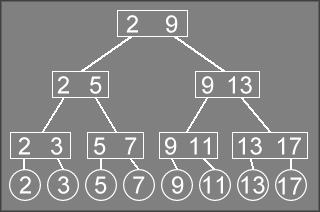
Since the insertion caused a sequence of splits that propagated all of the way to the root of the tree, it caused the depth of all leaf nodes in the tree to increase by one level.
Deletion
Deletion follows a similar track to insertion: It needs to recurse down to the leaf that contains the value, delete that value, then recurse back out and merge nodes.
One of the things that deletion needs to do is make certain that the low
keys in each node are up to date. This is important, since the merging
process can move children from one node into its sibling. The code uses
a brute-force hack to update all of the cached low keys for a node,
embodied in the FixLows() function.
void TwoThreeExterior::FixLows(TwoThreeExterior_t *pNode)
{
if (NULL != pNode) {
// If each child node exists, we can grab the Low1 key cached in
// in it, since cached keys are always kept updated.
// However, if this is a leaf, the child point will be NULL and the
// correct look-up key will be stored in Ref.
pNode->Low1 = (NULL != pNode->pChild1) ? pNode->pChild1->Low1
: pNode->pChild1->Ref.Key;
pNode->Low2 = (NULL != pNode->pChild2) ? pNode->pChild2->Low1
: 0;
pNode->Low3 = (NULL != pNode->pChild3) ? pNode->pChild3->Low1
: 0;
}
}
Another utility function used in deletion is ShiftChildrenDown(),
which is used to move children 2 and 3 down one slot after child 1 has been
remove from the node.
void TwoThreeExterior::ShiftChildrenDown(TwoThreeExterior_t *pNode)
{
pNode->pChild1 = pNode->pChild2;
pNode->pChild2 = pNode->pChild3;
pNode->pChild3 = NULL;
pNode->Low1 = pNode->Low2;
pNode->Low2 = pNode->Low3;
pNode->Low3 = 0;
}
The recursive logic for deletion is contained in DeleteRec.
Unlike insertion, the deletion logic will stop recursing when it reaches a
node whose children are leaves. Once it reaches the parent of the node to
delete, it will delete the child node, then shift any remaining children
down to replace the child pointer that was deleted. This may result in
pNode having only one child, which must be repaired after
returning from the current level of recursion.
DeleteRec returns a boolean, which indicates whether
pNode has only one child after deletion. This indicates that
the previous level of recursion needs to reshuffle child pointers or merge
child nodes.
bool TwoThreeExterior::DeleteRec(TwoThreeExterior_t *pNode, const U32 key)
{
// If we reach a leaf that does not contain the key for deletion,
// then we know that the key is not in the tree. No deletion needs
// to be returned, nor will the caller need to perform any fix-up
// operations. Return false so the caller knows no further work is
// required.
if (pNode->IsLeaf && (key != pNode->Ref.Key)) {
return false;
}
// We cannot be in a leaf if the key has not yet been found. That
// case is handled in the parent node of the leaf, since all of the
// fix-up work needs to be done in that node.
QzAssert(false == pNode->IsLeaf);
///////////////////////////////
// Deletion of leaf nodes. //
///////////////////////////////
// Special case: Child 1 is a leaf that contains the key to delete.
if ((NULL != pNode->pChild1) &&
(pNode->pChild1->IsLeaf) &&
(key == pNode->pChild1->Ref.Key))
{
// Delete the first child, then shift the two remaining children
// down. Since this is not a leaf node, it contains at least two
// children.
Free(pNode->pChild1);
ShiftChildrenDown(pNode);
// If the deletion resulted in this node having only one child,
// return true so fix-up operations can be performed on the parent.
return (NULL == pNode->pChild2);
}
// Special case: Child 2 is a leaf that contains the key to delete.
if ((NULL != pNode->pChild2) &&
(pNode->pChild2->IsLeaf) &&
(key == pNode->pChild2->Ref.Key))
{
// Delete the second child.
Free(pNode->pChild2);
// Shift the third child down to replace the second.
pNode->pChild2 = pNode->pChild3;
pNode->pChild3 = NULL;
// Third child is now a NULL reference.
pNode->Low2 = pNode->Low3;
pNode->Low3 = 0;
// If there is no second child, return true so fix-up operations
// can be applied to the parent node.
return (NULL == pNode->pChild2);
}
// Special case: Child 3 is a leaf that contains the key to delete.
if ((NULL != pNode->pChild3) &&
(pNode->pChild3->IsLeaf) &&
(key == pNode->pChild3->Ref.Key))
{
// This is the easiest case. Just delete the third node and return
// false. No fix-up operation will be required since we just turned
// a 3-node into a 2-node.
Free(pNode->pChild3);
pNode->pChild3 = NULL;
pNode->Low3 = 0;
return false;
}
//////////////////////////
// Fix-up operations. //
//////////////////////////
bool result = false;
// The key to delete is contained in the third child. The recursive
// call to DeleteRec() will remove the target node from the tree.
if ((NULL != pNode->pChild3) && (key >= pNode->Low3)) {
bool doFixup = DeleteRec(pNode->pChild3, key);
// If pChild3 ended up with only one child, we need to apply a
// fix-up operation so it will have two children.
if (doFixup) {
TwoThreeExterior_t *three = pNode->pChild3;
TwoThreeExterior_t *two = pNode->pChild2;
// The simple case is when child 2 has three children. We just
// need to move child 2's third child over to child 3. No
// deletion is required in this case.
if (3 == ChildCount(two)) {
// Three's child1 becomes child2.
three->pChild3 = three->pChild2;
three->pChild2 = three->pChild1;
// Two's child3 becomes three's child 1.
three->pChild1 = two->pChild3;
two->pChild3 = NULL;
// Directly fix up the low keys.
three->Low3 = three->Low2;
three->Low2 = three->Low1;
three->Low1 = two->Low3;
two->Low3 = 0;
}
// Otherwise child two only has 2 children, so we need to merge.
else {
// Three's only child become two's third child.
two->pChild3 = three->pChild1;
two->Low3 = three->Low1;
// Clear the pointer before we delete the node.
three->pChild1 = NULL;
Free(three);
// Fix this node, since it no longer has a third child.
pNode->pChild3 = NULL;
pNode->Low3 = 0;
}
}
// Repair the low key references to the children. This needs to
// always be performed, even if no fix-up was required for this
// node. If any fix-up was applied to the child node, its low
// keys may have changed, so we must propagate the updated low
// keys up the tree.
FixLows(pNode);
// We can always resolve merging or swapping at this level, so the
// caller does not need to do any more repair work.
return false;
}
// The node to delete is contained within the second child.
if ((NULL != pNode->pChild2) && (key >= pNode->Low2)) {
bool doFixup = DeleteRec(pNode->pChild2, key);
// If child 2 ended up with only one child, we need to either move a
// second node into child 2, or delete child 2.
if (doFixup) {
TwoThreeExterior_t *two = pNode->pChild2;
TwoThreeExterior_t *one = pNode->pChild1;
TwoThreeExterior_t *three = pNode->pChild3;
// If child 1 contains three nodes, we can move one of those nodes
// over to child 2.
if (3 == ChildCount(one)) {
// Two's child 1 becomes its child 2.
two->pChild2 = two->pChild1;
two->Low2 = two->Low1;
// One's child 3 becomes two's child 1.
two->pChild1 = one->pChild3;
two->Low1 = one->Low3;
// One no longer has a child 3.
one->pChild3 = NULL;
one->Low3 = 0;
}
// If child 3 has three nodes, we can move one of those nodes into
// child 2.
//
// Note that ChildCount() returns 0 if three does not exist, so we
// don't need extra testing logic here.
//
else if (3 == ChildCount(three)) {
// Three's child 1 becomes two's child 2.
two->pChild2 = three->pChild1;
two->Low2 = three->Low1;
// Three's other children shift down one to fill up the hole.
three->pChild1 = three->pChild2;
three->pChild2 = three->pChild3;
three->pChild3 = NULL;
three->Low1 = three->Low2;
three->Low2 = three->Low3;
three->Low3 = 0;
}
// Otherwise child 1 only has two nodes (and child 3 either has
// only two children, or it does not exist at all).
else {
// Two's only child becomes one's child 3.
one->pChild3 = two->pChild1;
one->Low3 = two->Low1;
// Clear the pointer so we can delete the node.
two->pChild1 = NULL;
Free(two);
// Child 3 may or may not exist. It is safe to copy it over
// to replace child 2, since at this stage we just need to
// fix up the pointers in this node.
pNode->pChild2 = pNode->pChild3;
pNode->Low2 = pNode->Low3;
pNode->pChild3 = NULL;
pNode->Low3 = 0;
// However, if there was no Child 3 before, then we've
// created a degenerate node. Return true if there is no
// Child 2 so that the caller knows it has fix-up work to do.
result = (NULL == pNode->pChild2);
}
}
// Repair the low key references to the children. This needs to
// always be performed, even if no fix-up was required for this
// node. If any fix-up was applied to the child node, its low
// keys may have changed, so we must propagate the updated low
// keys up the tree.
FixLows(pNode);
return result;
}
// Otherwise the node to delete exists under the first child. Let the
// recursive logic handle the deletion.
bool doFixup = DeleteRec(pNode->pChild1, key);
// If child 1 ended up with only one child, we need to fix it up so it
// has two children, or delete it.
if (doFixup) {
TwoThreeExterior_t *one = pNode->pChild1;
TwoThreeExterior_t *two = pNode->pChild2;
// If child 2 has three children, then we can move one of them
// over to fill in child 1.
if (3 == ChildCount(two)) {
// Child 2's first child is moved over to Child 1.
one->pChild2 = two->pChild1;
one->Low2 = two->Low1;
// Shift Child 2's other children down to fill up the hole.
two->pChild1 = two->pChild2;
two->pChild2 = two->pChild3;
two->pChild3 = NULL;
two->Low1 = two->Low2;
two->Low2 = two->Low3;
two->Low3 = 0;
}
// Otherwise Child 2 only has two children, so we have to merge
// Child 1 into child 2.
else {
// Shift Child 2's children up one to open up a hole.
two->pChild3 = two->pChild2;
two->Low3 = two->Low2;
two->pChild2 = two->pChild1;
two->Low2 = two->Low1;
// Child 1's only child is moved over to child 2.
two->pChild1 = one->pChild1;
two->Low1 = one->Low1;
// Clear the pointer so we can delete this node.
one->pChild1 = NULL;
Free(one);
// We've now made a hole in the current node, so we need to
// shift it's children down one to fill in the hole.
ShiftChildrenDown(pNode);
// If the current node has ended up with only one child, we
// need to return true so that the caller knows it needs to
// perform fix-up operations on the parent node.
result = (NULL == pNode->pChild2);
}
}
// Repair the low key references to the children. This needs to
// always be performed, even if no fix-up was required for this
// node. If any fix-up was applied to the child node, its low
// keys may have changed, so we must propagate the updated low
// keys up the tree.
FixLows(pNode);
return result;
}
The top-level Delete() function handles the special cases for
deleting the last node in the tree, and merging
the root node, which
simply amounts to deleting the current root and making its one remaining
child the new root.
void TwoThreeExterior::Delete(const U32 key)
{
// Special case for an empty tree.
if (NULL == m_pRoot) {
return;
}
// Special case for deleting the last node in the tree.
if (m_pRoot->IsLeaf &&(key == m_pRoot->Ref.Key)) {
Free(m_pRoot);
m_pRoot = NULL;
return;
}
// DeleteRec() will do all of the work. The only special effort needed
// is when m_pRoot ends up with a single child (that is not a leaf).
// If this happens, we need to delete the current root node and make its
// child the new root of the tree (which causes the depth of the tree to
// decrease by one level, and is the only way in which the depth of the
// leaves will change due to deletion).
//
if (DeleteRec(m_pRoot, key)) {
TwoThreeExterior_t *pTemp = m_pRoot;
m_pRoot = m_pRoot->pChild1;
pTemp->pChild1 = NULL;
Free(pTemp);
}
}
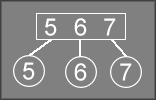
As an example of deletion, consider the following tree:
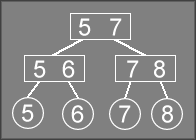
To delete the node 8
, DeleteRec will recurse down until it
finds the node containing 8
, producing the following call stack:
Delete("8")DeleteRec("5 7", "8")DeleteRec("7 8", "8")
Note that recursion will stop when it reaches the 7 8
node. The recursive
logic for deletion will never reach a leaf node; it always stops when it
reaches the parent of a leaf node.
DeleteRec will remove the 8
node, which creates a degenerate
1-node that contains only 7
. DeleteRec will then return
true to indicate that the node it just processed no longer
has two children.
At this point, the tree looks something like this:
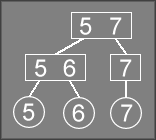
This will trigger the fix-up logic in the second half of DeleteRec,
while looking at the 5 7
node. Since child 1 (the 5 6
node) only has two
children, and child 3 does not exist, the only option is to merge child 2 (the 7
node) with child 1. This changes child 1 to contain 5 6 7
.
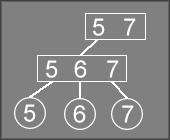
The clean-up logic will then remove the reference to 7
from the 5 7
node,
which turns that node into a degenerate 1-node:
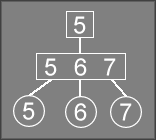
The resulting 5
node only has one child, so DeleteRec will
return true to indicate that the caller needs to do more fix-up
work on the tree.
Since Delete is the caller in this case, it fixs the problem by
deleting the degenerate 5
node and making 5 6 7
the new root of the tree.
This removes one level of the 2-3 tree, decreasing the depth of all leaf
nodes by one.