Overview
In this article, I will cover one possible implementation of red-black trees.
Working source code and a test app can be found in balanced_tree.zip.
Since working source code a rare beast indeed where red-black trees are concerned, the code for this article is based on Julienne Walker's description, ported to C++ and commented. After much googling around, Julienne's article was the only one that I found complete enough to implement, and clear enough for me to understand.
Why write up another article, when the one above does an adequate job? Partly to convince myself I understand how red-black trees work, and partly for testing. As covered in the final article in this series, I wanted to do some performance testing to measure for myself how well these different algorithms perform. In the end, I found internal 2-3 trees to be the best for my needs, but it was useful to test different implementations.
Red-Black Trees
Red-black trees suffer from differing descriptions, some of which I consider
to be implementation dependent
. The basic rules are:
- The root is black.
- A red node's parent is black.
- A red node is either a leaf, or it has two black children.
- Every path from the root to a leaf must pass through the same number of black nodes.
- A black node that is not a leaf has either
- two black children,
- one red child and one black child, ¹
- or a single child, which is a red leaf.
¹ This rule is not always enforced. Many implementations (including this one) will allow a black node to have two red children.
These are a synthesis of the rules described in
Lewis and Denenberg, Data Structures and Their Algorithms, and
Cormen, Leiserson, Rivest, and Stein, Introduction to Algorithms.
Neither source provides what I would consider a clear description of the
algorithm. Lewis and Denenberg hand-wave it with incomplete pseudo-code,
while Cormen et al. obfuscate things with proofs and lemmas.
Cormen et al. do at least provide pseudo-code for deletion, which
is remarkable — text books generally leave balanced tree deletion as an
exercise for the reader
. That may be good enough for the class room,
but fails those of us who need a complete working reference.
Having described two different implemetations of 2-3 trees in previous articles, I find the easiest way to explain red-black trees is to start with a simple 2-3 tree:
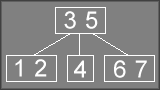
We can then color all of the elements so that the first key in each 2-3 node is black, while the second key is red. Then draw lines between all of the keys: horizontal lines are red, vertical lines are black:
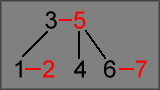
Once all of the nodes have been repositioned into a standard binary tree layout, we now have a normal-looking red-black tree:
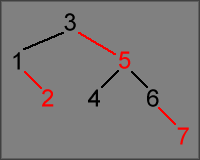
In other words, a red-black tree is a means of storing a 2-3 tree in a binary tree, using arbitrary colors to distinguish 3-nodes from parent-child links: black nodes contain the first value of a 2-node or 3-node, red nodes contain the second value of a 3-node.
When drawn out as a diagram, coloring the values in red and black helps visualize the underlying 2-3 tree. However, when used in code, the nodes could just as well be labeled lemon and lime (I vanted orange!) for all the good they do in adding meaning to the tree. Maybe I'm getting too old, but cryptic code names and one-letter variables lost their appeal long, long ago.
One of the motivations for red-black trees was to avoid wasted storage space, and to simplify code for doing look-ups — searching a binary tree is a very simple algorithm. In a 2-3 tree, nodes contain extra space for a third pointer and a second data value, whereas no space is wasted in a red-black tree. In principle, this should make red-black trees more efficient — red-black trees try to obtain performance at the cost of extra complexity. As covered in the final article in this series, red-black trees are not necessarily faster, and can actually be slower than 2-3 trees.
Data Structures
For testing purposes, my code defines a simple VoidRef_t structure.
All look-up operations use a 32-bit integer for the search key, storing a
void* pointer to hold the value associated with the key.
struct VoidRef_t
{
U32 Key;
void* pContext;
};
Each node in the tree uses the RedBlackBasic_t structure.
This only needs to store the left/right child pointers, and a flag to
indicate whether this node is colored red or black.
struct RedBlackBasic_t
{
VoidRef_t Ref;
bool IsRed;
RedBlackBasic_t *pChild[2];
};
Rotation
To maintain balance in the tree, insertions and deletions will fix red-black violations (when a red node has another red node as a child) by rotating nodes:
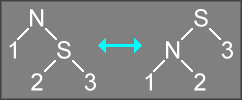
The rotation will change the positions of the N and S nodes, but the result of the rotation is still a correctly sorted binary tree. This is done any time the red/black coloring rules of a the tree are violated: e.g., if both N and its parent node are red (and S is black), a rotation will fix the rule violation. The trick at the heart of both insertions and deletions is to determine where to apply the rotation to fix the rule violation.
The logic for this is implemented in SingleRotation:
static RedBlackBasic_t* SingleRotation(RedBlackBasic_t *pNode, int dir)
{
RedBlackBasic_t *pSave = pNode->pChild[!dir];
pNode->pChild[!dir] = pSave->pChild[dir];
pSave->pChild[dir] = pNode;
pNode->IsRed = true;
pSave->IsRed = false;
return pSave;
}
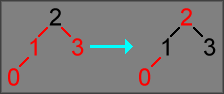
As implemented, rotation operations will also change the color of nodes. When
fixing a case where a red node has a red child, in some cases the code will simply
change the color assigned to each node to fix a red violation (a color flip
),
without performing any rotation:
In other cases, it will perform a rotation using SingleRotation,
then change the colors of some of the nodes:
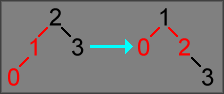
If you're paying attention, you should notice a problem with this rotation:
after the rotation and color changes are applied, both children of 1
are red nodes.
This is a violation of one of the rules of red-black trees: at most one child of a
black node can be red. This is a convention of Julienne Walker's implementation, and
also occurs in many other implementations of red-black trees. Relaxing this rule can
reduce the amount of fix-up code required to handle red violations: this makes the code
faster, but the implementation ceases to be equivalent to a 2-3 tree (it is now possible
to have 4-nodes in the tree, making the tree equivalent to a 2-3-4 tree; any node with
two red children is a 4-node).
The DoubleRotation function applies two rotations, alternating the
direction of the two rotations. Consider the following case:
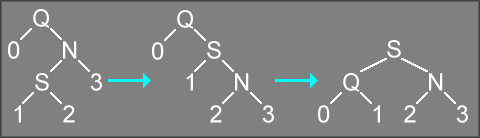
Calling DoubleRotation("Q", 0) on the above tree is equivalent to
calling SingleRotation("N", 1) followed by SingleRotation("Q", 0).
This makes nodes Q, N, and S more balanced (and also directly modifies the red/black
setting of each node).
Likewise, passing a 1 to DoubleRotation instead of a
0 would produce the following operation:
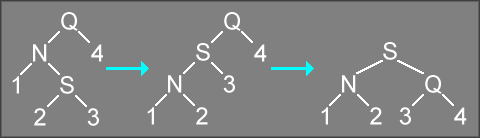
In this case, calling DoubleRotation("Q", 1) on the above tree
is equivalent to calling SingleRotation("N", 0) followed by
SingleRotation("Q", 1).
static RedBlackBasic_t* DoubleRotation(RedBlackBasic_t *pNode, int dir)
{
pNode->pChild[!dir] = SingleRotation(pNode->pChild[!dir], !dir);
return SingleRotation(pNode, dir);
}
Insertion
The form of insertion used is top-down, which can be implemented iterative instead of recursively.
void RedBlackBasic::Insert(VoidRef_t ref)
{
// The standard case is inserting into a non-empty tree.
if (NULL != m_pRoot) {
// Use a dummy placeholder to initialize the traversal pointers.
// This will simplify looping logic, since it makes certain that
// the pointers are never NULL even when looking at the root of
// the tree. This eliminates the need for special-case handling
// of NULL pointers in the inner loop below.
RedBlackBasic_t head = {0};
int prevDir = 0;
int currDir = 0;
head.pChild[1] = m_pRoot;
// Use a couple pointers to traverse through the binary tree.
// Also record the previous value for each of these pointers,
// which are needed to update child pointers in the parent nodes.
RedBlackBasic_t *pParentPrev = &head;
RedBlackBasic_t *pParentCurr = NULL;
RedBlackBasic_t *pEnumPrev = NULL;
RedBlackBasic_t *pEnumCurr = m_pRoot;
// Use an infinite loop for traversing the tree. There is an ending
// condition, but that condition is most easily tested in the middle
// of the loop.
for ( ; ; ) {
// Once we hit a leaf node, insert the value below the last node
// that was examined (pEnumPrev is the parent of pEnumCurr).
if (NULL == pEnumCurr) {
pEnumCurr = NewNode();
pEnumPrev->pChild[currDir] = pEnumCurr;
pEnumCurr->Ref = ref;
// NOTE: Even though we have inserting the new value into
// the tree, we do not break out of the loop. We still need
// to execute some more code to fix any red violations that
// were introduced by the insertion.
}
// Only one child of a black node can be red. If we encounter a
// node where both children are red, we have placed the tree in
// an invalid state. Apply a color flip to force the current
// node to be red and make both of its children black.
else if (IsRed(pEnumCurr->pChild[0]) &&
IsRed(pEnumCurr->pChild[1]))
{
pEnumCurr->IsRed = true;
pEnumCurr->pChild[0]->IsRed = false;
pEnumCurr->pChild[1]->IsRed = false;
}
// A red violation occurs if the both the current node and its
// parent are red. This indicates that the tree is not properly
// balanced. Apply a rotation to rebalance this part of the
// tree, which will also fix the red violation.
if (IsRed(pEnumCurr) && IsRed(pEnumPrev)) {
int dir2 = (pParentPrev->pChild[1] == pParentCurr);
if (pEnumCurr == pEnumPrev->pChild[prevDir]) {
pParentPrev->pChild[dir2]
= SingleRotation(pParentCurr, !prevDir);
}
else {
pParentPrev->pChild[dir2]
= DoubleRotation(pParentCurr, !prevDir);
}
}
// If we see the key we're trying to write, we can break out
// of the loop. In most cases the key was just inserted, and
// this code is being applied after fixing any red violations.
// However, it is possible that the key was already stored in
// the tree, so we need to write the key/value pair again to
// handle the case where an existing key is being updated with
// a new value.
if (pEnumCurr->Ref.Key == ref.Key) {
pEnumCurr->Ref = ref;
break;
}
// Keep track of whether we traversed left or right on the
// previous iteration, so we know which child pointer to update.
prevDir = currDir;
currDir = pEnumCurr->Ref.Key < ref.Key;
// Keep track of the previous parent pointer so we can update
// its child pointers on subsequent iterations.
if (NULL != pParentCurr) {
pParentPrev = pParentCurr;
}
pParentCurr = pEnumPrev;
pEnumPrev = pEnumCurr;
pEnumCurr = pEnumCurr->pChild[currDir];
}
// If rotations propagated all the way to the root, the updated
// root pointer will now be stored in the dummy structure.
m_pRoot = head.pChild[1];
}
// Special case for inserting into an empty tree.
else {
m_pRoot = NewNode();
m_pRoot->Ref = ref;
}
// Rotations may have resulted in a red node becoming the root of the
// tree. Force the root node to always be black to conform with the
// rules of a red-black tree.
m_pRoot->IsRed = false;
}
Deletion
The form of deletion used is top-down, which can be implemented iterative instead of recursively.
void RedBlackBasic::Delete(const U32 key)
{
if (NULL == m_pRoot) {
return;
}
// Use a dummy placeholder to initialize the traversal pointers.
// This will simplify looping logic, since it makes certain that
// the pointers are never NULL even when looking at the root of
// the tree. This eliminates the need for special-case handling
// of NULL pointers in the inner loop below.
RedBlackBasic_t head = {0};
RedBlackBasic_t *pPrev = NULL;
RedBlackBasic_t *pCurr = NULL;
RedBlackBasic_t *pScan = &head;
RedBlackBasic_t *pFound = NULL;
head.pChild[1] = m_pRoot;
int prevDir = 1;
int currDir = 1;
// Keep scanning until we hit a leaf. Once we find a leaf, the
// key stored in that leaf can be used to replace the key to be
// deleted (assuming that the target key is found in the tree).
while (NULL != pScan->pChild[currDir]) {
pPrev = pCurr;
pCurr = pScan;
pScan = pScan->pChild[currDir];
prevDir = currDir;
currDir = (pScan->Ref.Key < key);
// If we found the key to be deleted, record which node contains
// it. This value will need to be replaced with another key (the
// in-order successor of the key to delete), but we won't know
// what value to use until we have exited this loop.
if (pScan->Ref.Key == key) {
pFound = pScan;
}
// Traverse down black links in the tree.
//
// Red nodes are not ignored. Instead, they are processed
// from their parent node (which is always a black node).
//
if ((false == IsRed(pScan)) &&
(false == IsRed(pScan->pChild[currDir])))
{
// Once we get into this code block, we know that pScan is a
// black node. Since currDir indicates which child will be
// processed next, we need to check the other child (!currDir).
//
// If the opposite child is red, then the deletion may cause
// the target child to be turned into a red node. Since a
// black node may not have two red children, we need to apply
// a rotation to the opposite child to fix this.
//
if (IsRed(pScan->pChild[!currDir])) {
// A rotation is needed to avoid red violations. Since
// the rotation changes the local arrangement of the tree,
// we also need to update pCurr to keep proper track of
// how we reached this node.
pCurr->pChild[prevDir] = SingleRotation(pScan, currDir);
pCurr = pCurr->pChild[prevDir];
}
// Otherwise the target node is black, so we need to examine
// its children, fix coloring to avoid red violations, and
// possibly rotate part of the tree to rebalance the tree to
// prepare for removing a node.
else {
RedBlackBasic_t *pTemp = pCurr->pChild[!prevDir];
if (NULL != pTemp) {
// If we end up with this particular arrangement of all
// black nodes, we can safely convert a couple of them
// to be red nodes without introducing a red violation.
if ((false == IsRed(pTemp->pChild[0])) &&
(false == IsRed(pTemp->pChild[1])))
{
pCurr->IsRed = false;
pTemp->IsRed = true;
pScan->IsRed = true;
}
// Otherwise one of the children is red. If a red
// violation is detected, we have to fix the violation
// by applying a rotation to the current node.
else {
int tempDir = (pPrev->pChild[1] == pCurr);
if (IsRed(pTemp->pChild[prevDir])) {
pPrev->pChild[tempDir] = DoubleRotation(pCurr, prevDir);
}
else if (IsRed(pTemp->pChild[!prevDir])) {
pPrev->pChild[tempDir] = SingleRotation(pCurr, prevDir);
}
// Mark all of these nodes to have a safe
// arrangement of red and black that cannot
// possibly have red violations.
pScan->IsRed = true;
pPrev->pChild[tempDir]->IsRed = true;
pPrev->pChild[tempDir]->pChild[0]->IsRed = false;
pPrev->pChild[tempDir]->pChild[1]->IsRed = false;
}
}
}
}
}
// Now that we have finished scanning the tree, we know
// whether or not the search key is present in the tree.
//
// If the key is in the tree, we can remove the key by replacing it
// with the value in pScan. Since pScan is guaranteed to be a leaf
// node, we then delete that node, since it is no longer needed in
// the tree.
if (NULL != pFound) {
pFound->Ref = pScan->Ref;
pCurr->pChild[pCurr->pChild[1] == pScan] = pScan->pChild[pScan->pChild[0] == NULL];
Free(pScan);
}
// Rotations may have propagated back to the root of the tree.
// If so, the new root pointer is cached in the dummy structure.
m_pRoot = head.pChild[1];
// The root of a red-black tree must always be black. It is safe to
// mark the root as always being black to satisfy this requirement.
if (NULL != m_pRoot) {
m_pRoot->IsRed = false;
}
}