Balanced Trees, Part 2:
Interior 2-3 Trees

Overview

Data Structures

For evaluation purposes, I define a simple key-value pair, where data is sorted with an unsigned 32-bit integer. The value is a blind void* pointer. This pointer is not used for testing, it is simply the value returned when doing a look-up operation in the resulting binary tree.

struct VoidRef_t
{
    U32   Key;
    void* pContext;
};

Each node in the tree uses the following structure:

struct TwoThreeInterior_t
{
    TwoThreeInterior_t *pChild1;
    TwoThreeInterior_t *pChild2;
    TwoThreeInterior_t *pChild3;

    VoidRef_t RefLo;
    VoidRef_t RefHi;
};

Rotation

When a 2-3 tree is placed in an inconsistent state — typically due to converting a node into 1-node or a 4-node (neither of which is permitted in a 2-3 tree) — the most common fix is to apply a rotation.

To demonstrate rotation, consider the following tree:

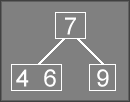
To insert a 5 into the tree, we traverse down to the 4 6 node. If we were to insert the 5 into this node, we would end up with a node having three values (which means it would have 4 children if it were not a leaf, so it would be called a 4-node).

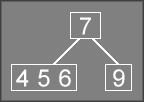
Since 4-nodes are not permitted, we have to rebalance the tree. In this case, the node containing 9 is a 2-node, so we have somewhere to store the extra value.

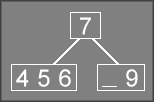
To prepare for the rotation, the 9 is moved over to be the second value in the node, leaving the first one empty.

Then the rotation is applied by moving the 7 down to fill the empty space, then moving the 6 up to the parent node to where the 7 was previously stored.

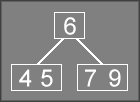
The final result is a balanced 2-3 tree.

Insertion

Insertions involve various special cases that must be addressed to rebalance the tree once a new value has been stored in a node. The Insert function serves as the main entry point for inserting a new value into the tree. Insert is mostly just responsible for handling the special case of splitting the root of the tree. The bulk of the work is handled recursively with InsertRec.

For an example of insertion, consider the following 2-3 tree:

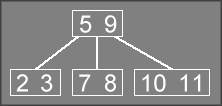
If we try to insert a 6 into the tree, the recursion will traverse the 5 9 and 7 8 nodes. At the bottom of recursion, the call stack will look something like this:

• Insert("6")
• InsertRec("5 9", "6")
• InsertRec("7 8", "6")

At the bottom of recursion, InsertRec will want to insert the 6 to produce a tree that looks like this:

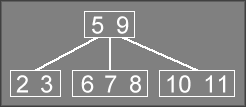
However, the node that would contain the 6 7 8 is illegal, since 4-nodes are not allowed in the tree. Instead, InsertRec will remove this node from the tree, storing the 6 in it (this pointer is returned in the ppN1 pointer). A new node will be created to hold the 8 (this pointer is returned in ppN2), and the value 7 will be returned in the ref parameter.

When this call to InsertRec returns, the incomplete tree looks something like this:

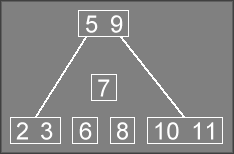
Upon returning to the previous level of recursion, InsertRec will see that it has an incomplete tree that needs to be repaired.

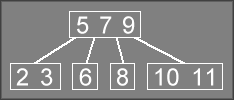
Conceptually, it will attempt to repair the tree by creating a node that contains 5 7 9. Again, this is a 4-node, which is not allowed in a 2-3 tree.

Instead, similar logic is applied to move the 5 and 9 into separate nodes (returned in ppN1 and ppN2, and the 7 is returned in the ref parameter).

When we return from the next level of InsertRec, the tree is still incomplete and is arranged something like this:

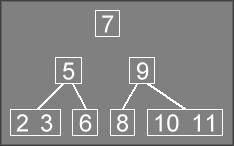
At this point, we are back in the original call to Insert, which needs to repair the tree. This is accomplished by allocating a new root node, setting the 7 to be the root of the tree, with the 5 and 9 as the first two children of the new root.

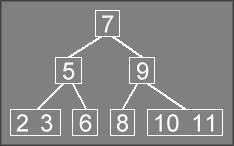
Because this insertion caused the root node to be split, it increased the height (or depth, depending on your preferred term) of the tree. Splitting the root like this is the only way that the height of the tree can increase.

This is the implementation of the main Insert method:

void TwoThreeInterior::Insert(VoidRef_t ref)
{
    // In the normal case, the tree is not empty.
    if (NULL != m_pRoot) {
        TwoThreeInterior_t *pN1  = NULL;
        TwoThreeInterior_t *pN2  = NULL;

        // If the recursive operation returns true, we need to split the
        // root of the tree.  The existing root node has already been
        // changed to maintain sorting order (the current root pointer is
        // returned in pN1), and a new node is returned in pN2.  Since
        // all conditioning was done by the recursive routine, all we
        // need to do is create a new root node and make the two pointers
        // the children of the new root node.
        //
        // Also note that ref is pass-by-reference, so upon exiting the
        // recursive function, ref will now contain the correct key for
        // the new root node.
        //
        if (InsertRec(m_pRoot, ref, &pN1, &pN2)) {
            m_pRoot = NewNode();

            m_pRoot->RefLo   = ref;
            m_pRoot->pChild1 = pN1;
            m_pRoot->pChild2 = pN2;
        }
    }

    // Special case for inserting into an empty tree.
    else {
        m_pRoot = NewNode();
        m_pRoot->RefLo  = ref;
    }
}

As can be seen, the Insert method does very little work. It is only responsible for splitting the root, or inserting a key into an empty tree.

The bulk of the insertion logic is contained in InsertRec, which is an inherently recursive method. This method does all of the work for locating the position where the insertion should occur, rearranging the contents of the tree, and returning info needed by the caller to perform a split.

If the node ends up being split, this method will return true, so the caller knows it needs to finish the splitting logic. This method cannot do the split itself, since it does not have a reference to the parent node. This is a necessity to generalize the code to also handle the root of the tree. Because the root does not have a parent, it is more simple to create a new node (if necessary), return that in ppN2, and let the caller handle creating a new node to contain the split.

If a split is required, this code will rearrange data to guarantee that all values stored in ppN1 and ppN2 are sorted, that ppN1 will be positioned to the left (less-than) of ppN2, and that ref will be modified to hold the key that falls between ppN1 and ppN2.

This means that the contents of pNode will be changed when a split is required. Technically, this operation could be considered destructive, but it is necessary to assure that the two sibling nodes at this level are organized correctly. It also makes it easy for the caller to finish the split by allocating a new node, making ppN1 and ppN2 its two children, and setting returned ref.Key as the key that comes between the two modified nodes.

bool TwoThreeInterior::InsertRec(TwoThreeInterior_t *pNode,
                                 VoidRef_t          &ref,
                                 TwoThreeInterior_t **ppN1,
                                 TwoThreeInterior_t **ppN2)
{
    TwoThreeInterior_t *pN1  = NULL;
    TwoThreeInterior_t *pN2  = NULL;
    TwoThreeInterior_t *pNew = NULL;

    VoidRef_t key[3];

    // If a split operation occurs, we'll have to turn a 3-node into a
    // 4-node.  However, there is no such thing as a 4-node in a 2-3
    // tree.  This array is used as a placeholder while rearranging the
    // four nodes in the correct order.
    TwoThreeInterior_t *pC[4];

    // This is an internal node.  We need to start off by recursing down
    // to the appropriate child.  If the recursion caused a split, we
    // need to finish the split logic here.
    if (NULL != pNode->pChild1) {

        // Recurse down the first child.
        if (ref.Key < pNode->RefLo.Key) {
            if (false == InsertRec(pNode->pChild1, ref, &pN1, &pN2)) {
                return false;
            }

            // A split of the child nodes was performed.  Figure out what
            // work is needed to clean up at this level.

            // If this is a 2-node, we just need to rearrange the keys and
            // child pointers.
            //
            // Since we recursed down the left, the second child remains
            // unchanged.  All we need to do for it is shift it over to
            // become the third child.
            //
            // Then we poke the returned values in as the first and second
            // child.
            //
            // In this case, the splitting is now contained, so we return
            // false.
            //
            if (NULL == pNode->RefHi.pContext) {
                pNode->RefHi   = pNode->RefLo;
                pNode->RefLo   = ref;
                pNode->pChild3 = pNode->pChild2;
                pNode->pChild2 = pN2;
                pNode->pChild1 = pN1;

                return false;
            }

            // Otherwise we need to convert this 3-node into a 4-node.
            // Poke the values into the arrays so the clean-up logic can
            // split this node.
            else {
                key[0] = ref;
                key[1] = pNode->RefLo;
                key[2] = pNode->RefHi;
                pC[0]  = pN1;
                pC[1]  = pN2;
                pC[2]  = pNode->pChild2;
                pC[3]  = pNode->pChild3;
            }
        }

        // If this is a 3-node, we need to decide whether to recurse down
        // the second or third child.
        else if (NULL != pNode->RefHi.pContext) {

            // Recurse down the middle child.
            if (ref.Key < pNode->RefHi.Key) {
                if (false == InsertRec(pNode->pChild2, ref, &pN1, &pN2)) {
                    return false;
                }

                // The recursive call caused a split.  Since we now have a
                // 4-node, we have no choice but to split this node as well.
                key[0] = pNode->RefLo;
                key[1] = ref;
                key[2] = pNode->RefHi;
                pC[0]  = pNode->pChild1;
                pC[1]  = pN1;
                pC[2]  = pN2;
                pC[3]  = pNode->pChild3;
            }

            // Recurse down the third child.
            else if (ref.Key > pNode->RefHi.Key) {
                if (false == InsertRec(pNode->pChild3, ref, &pN1, &pN2)) {
                    return false;
                }

                key[0] = pNode->RefLo;
                key[1] = pNode->RefHi;
                key[2] = ref;
                pC[0]  = pNode->pChild1;
                pC[1]  = pNode->pChild2;
                pC[2]  = pN1;
                pC[3]  = pN2;
            }

            else {
                pNode->RefHi = ref;
                return false;
            }
        }

        // Otherwise this is a 2-node, so we can only recurse down the
        // middle child.
        else if (ref.Key > pNode->RefLo.Key) {
            if (false == InsertRec(pNode->pChild2, ref, &pN1, &pN2)) {
                return false;
            }

            // A split occurred.  However, since this is a 2-node, the split
            // is contained to this level of the tree.  Since the recursive
            // call did all of the rearranging work, we replace the current
            // key and pointers with the values returned from the recursive
            // call.
            pNode->RefHi   = ref;
            pNode->pChild2 = pN1;
            pNode->pChild3 = pN2;

            return false;
        }

        else {
            pNode->RefLo = ref;
            return false;
        }
    }

    // Recursive base case:  This is where we hit a leaf node.  Unless
    // the key is found in this node, we will try to insert the new
    // key in this node, possibly causing a split.
    else {
        // This leaf only contains one key.  No split is required, we just
        // need to insert the new key into the correct place (or replace
        // an existing value).
        if (NULL == pNode->RefHi.pContext) {

            // If the new key is bigger than the one key in this node,
            // it becomes the second key.
            if (ref.Key > pNode->RefLo.Key) {
                pNode->RefHi = ref;
            }

            // Otherwise we need to shift the existing key over to be
            // the second key, then drop the new key in as the first key.
            else if (ref.Key < pNode->RefLo.Key) {
                pNode->RefHi = pNode->RefLo;
                pNode->RefLo = ref;
            }

            // Otherwise we're replacing an existing key with a new value.
            // This does not insert a new value, it only replaces the
            // existing value.  
            else {
                pNode->RefLo = ref;
            }

            // No split was required, so no fix-up operations will be
            // required as we back out of the recursion.
            return false;
        }

        // Otherwise splitting is required.  We don't need to deal with
        // any pointers, since there are no child nodes, but we do need to
        // rearrange the existing keys so that they are correctly sorted.
        //
        // Note the special cases where the key being replaced matches a
        // key already present.  Here we just need to replace the old key,
        // under the assumption that its value has been updated.

        if (ref.Key < pNode->RefLo.Key) {
            key[0] = ref;
            key[1] = pNode->RefLo;
            key[2] = pNode->RefHi;
        }

        // Special case: replace an existing value.
        else if (ref.Key == pNode->RefLo.Key) {
            pNode->RefLo = ref;
            return false;
        }

        else if (ref.Key < pNode->RefHi.Key) {
            key[0] = pNode->RefLo;
            key[1] = ref;
            key[2] = pNode->RefHi;
        }

        // Special case: replace an existing value.
        else if (ref.Key == pNode->RefHi.Key) {
            pNode->RefHi = ref;
            return false;
        }

        else {
            key[0] = pNode->RefLo;
            key[1] = pNode->RefHi;
            key[2] = ref;
        }

        // Since this is a leaf node, leave all child pointers NULL.
        pC[0] = NULL;
        pC[1] = NULL;
        pC[2] = NULL;
        pC[3] = NULL;
    }


    // The remaining code is only executed if we have created a 4-node.
    // This forces pNode to be split.  The code above has already stored
    // the keys and child pointers in the correct order.

    // Destructively replace the contents of pNode to contain the first
    // two child nodes.
    pNode->RefLo          = key[0];
    pNode->RefHi.Key      = 0;
    pNode->RefHi.pContext = NULL;
    pNode->pChild1        = pC[0];
    pNode->pChild2        = pC[1];
    pNode->pChild3        = NULL;

    // Create a new node to contain the last two child pointers.
    pNew = NewNode();
    pNew->RefLo           = key[2];
    pNew->pChild1         = pC[2];
    pNew->pChild2         = pC[3];
    pNew->pChild3         = NULL;

    // Return the info about these two sibling nodes so the caller can
    // handle the split at its level.
    ref   = key[1];
    *ppN1 = pNode;
    *ppN2 = pNew;

    return true;
}

Deletion

As an example of deletion, consider the following 2-3 tree:

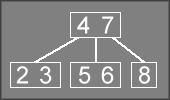
To delete 5 from the tree, all the code needs to do is convert the 5 6 node into a 2-node containing only a 6. No merging or rotation is required to apply this transform.

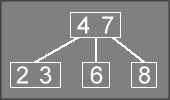
If we then delete 6 from the tree, we end up with a degenerate node. This can be fixed by performing a rotation on the tree, rotating the 4 down to the empty node, then rotating the 3 up to replace the 4.

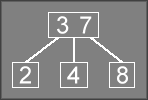
To delete the 4 from the tree, we have to merge two nodes. This specific example will invoke the code in FixSecond (described further down), which will merge the empty node with the node containing the 8. This particular merge operation will rotate the 7 down to fill in the empty node, then merge that node with the 8, producing the following tree:

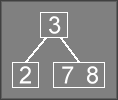
To delete the 2 from the tree, another rotation is applied to first rotate the 3 down into the empty node, then rotate the 7 up to replace the 3.

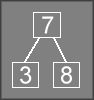
All deletion operations are accomplished by one of three general cases:

• Deleting a key from a 3-node: Just convert the node into a 2-node.
• Deleting a key from a 2-node:
  • Rotate a value in from an adjacent 3-node, or
  • Merge with an adjacent 2-node, and rotate a key in from the parent node.

The following support routines are needed to assist deletions from the tree.

One operation is the need to find an in-order successor. This routine is needed for certain special cases, and answers the question: Given a key n, what is the smallest key value that is greater than n?

The InOrderSuccessor is a destructive operation. It follows the leftmost child of each node until it reaches a leaf node. The lowest value in this leaf node is the in-order successor. Once this node is found, InOrderSuccessor will return that value in the ref parameter, NULLing out the previous value.

This places the tree in an invalid state. After InOrderSuccessor has completed, the code will need to repair all of those nodes. This is done by recursively calling FixInOrderSuccessor, which will recurse down the leftmost pointer of each node until it finds the location where the in-order successor was previous stored. FixInOrderSuccessor will then recurse back out, calling FixFirst to repair the damage to the tree.

/////////////////////////////////////////////////////////////////////////////
//
//  InOrderSuccessor()
//
//  Given a key, find the smallest key that comes immediately after
//  this node.  This simply amounts to finding the leftmost child.
//
//  Since this code is used specifically for deletion, it will swap the
//  in-order successor into the given node, and place the old value of the
//  current node in ref.  This simplifies the swapping logic needed when
//  merging nodes.
//
bool TwoThreeInterior::InOrderSuccessor(TwoThreeInterior_t *pNode, VoidRef_t &ref)
{
    // Keep traversing until we hit a leaf node.
    while (NULL != pNode->pChild1) {
        QzAssert(NULL != pNode);

        pNode = pNode->pChild1;
    }

    // Return the old value stored in pNode.
    ref = pNode->RefLo;

    pNode->RefLo          = pNode->RefHi;
    pNode->RefHi.Key      = 0;
    pNode->RefHi.pContext = NULL;

    return (NULL == pNode->RefLo.pContext);
}


/////////////////////////////////////////////////////////////////////////////
//
//  FixInOrderSuccessor()
//
//  If an in-order successor was found, InOrderSuccessor() will have modified
//  the contents of a node, leaving it in a broken state.  This method will
//  recurse down the tree and repair the damage using successive calls to
//  FixFirst().
//
bool TwoThreeInterior::FixInOrderSuccessor(TwoThreeInterior_t *pNode)
{
    if (NULL == pNode->pChild1) {
        return true;
    }

    // If this call returns true, the first child needs to be removed from
    // the tree.
    if (FixInOrderSuccessor(pNode->pChild1)) {
        return FixFirst(pNode);
    }

    return false;
}

More support is required from a trio of methods named FixFirst, FixSecond, and FixThird. These methods are used when the first, second, or third child of a node has been turned into a 1-node (a node with no value and at most one child pointer).

FixFirst and FixThird will attempt to repair the node by rotating a spare value in from the second child, but this only works if the second child is a 3-node (a node containing 2 keys). If the second child is a 2-node, the only option is to merge the two nodes.

FixSecond is more complex, since it has more options. If either the first or third child is a 3-node, this code can rotate the extra value in to fix the node. Otherwise it must pick one of the two adjacent nodes and perform a merge.

When any of these three methods is applied to a node, it will fix that node's child, but may have to turn pNode into a 1-node to apply the fix. If this happens, the method returns true, indicating that the caller needs to apply a fix to the parent node as well.

/////////////////////////////////////////////////////////////////////////////
//
//  FixFirst()
//
//  This is called when pNode->pChild1 has ended up as a degenerate 1-node.
//
//  If pNode->pChild2 is a 3-node, the nodes can be rebalanced by rotating
//  one of the keys from pChild2 to pChild1.
//
//  Otherwise the code has to merge pChild1 and pChild2.  If pNode only
//  had two children before the merge, this will cause pNode to become a
//  degenerate 1-node.
//
//  Returns true if pNode ends up with only one child after the merge.
//
bool TwoThreeInterior::FixFirst(TwoThreeInterior_t *pNode)
{
    TwoThreeInterior_t *pC1 = pNode->pChild1;
    TwoThreeInterior_t *pC2 = pNode->pChild2;

    // If pChild2 is a 3-node, we rotate one of its children over to
    // pChild1.  No merge is needed, so the fix-up work on the tree is
    // now complete.
    if (NULL != pC2->RefHi.pContext) {
        pC1->RefLo   = pNode->RefLo;
        pNode->RefLo = pC2->RefLo;
        pC2->RefLo   = pC2->RefHi;
        pC2->RefHi.Key      = 0;
        pC2->RefHi.pContext = NULL;
        pC1->pChild2 = pC2->pChild1;
        pC2->pChild1 = pC2->pChild2;
        pC2->pChild2 = pC2->pChild3;
        pC2->pChild3 = NULL;

        return false;
    }

    // If we get to here, pChild2 is a 2-node.  We have no choice but to
    // merge pChild1 and pChild2.

    // The first key in pNode and the only key in pChild2 are moved into
    // pChild1, turning pChild1 into a 3-node.
    pC1->RefLo = pNode->RefLo;
    pC1->RefHi = pC2->RefLo;
    pC2->RefLo.Key      = 0;
    pC2->RefLo.pContext = NULL;

    // The two children of pChild2 are moved into pChild1.
    pC1->pChild2 = pC2->pChild1;
    pC1->pChild3 = pC2->pChild2;

    // Clear out the pointers to avoid problems with freeing pChild2.
    pC2->pChild1 = NULL;
    pC2->pChild2 = NULL;
    pC2->pChild3 = NULL;

    // pChild3 becomes pChild2.  This may turn pNode into a degenerate
    // 1-node.
    pNode->RefLo = pNode->RefHi;
    pNode->RefHi.Key      = 0;
    pNode->RefHi.pContext = NULL;
    pNode->pChild2 = pNode->pChild3;
    pNode->pChild3 = NULL;

    Free(pC2);

    // Following the merge, pNode may have turned into a 1-node.  Return
    // true if the merge needs to propagate up the tree.
    return (NULL == pNode->RefLo.pContext);
}


/////////////////////////////////////////////////////////////////////////////
//
//    FixSecond()
//
//    This is called when pNode->pChild2 has ended up as a degenerate 1-node.
//
//    This is the most complex of the fix-up routines.  If either pChild1 or
//    pChild3 is a 3-node, the extra node can be rotated into pChild2 to turn
//    it back into a 2-node.  If we cannot rotate a value in from a sibling,
//    we will be forced to merge pChild1 and pChild2.
//
//    Returns true if pNode ends up as a 1-node, which forces the fix-up
//    operation to propagate up to the next level of the tree.
//
//    NOTE: This pNode is never a leaf node.  Before this call, the node is
//    legal and has at least two children.
//
bool TwoThreeInterior::FixSecond(TwoThreeInterior_t *pNode)
{
    TwoThreeInterior_t *pC1 = pNode->pChild1;
    TwoThreeInterior_t *pC2 = pNode->pChild2;
    TwoThreeInterior_t *pC3 = pNode->pChild3;

    // If pChild3 exists and is a 3-node, rotate a value over to pChild2.
    if ((NULL != pC3) && (NULL != pC3->RefHi.pContext)) {
        pC2->RefLo   = pNode->RefHi;
        pNode->RefHi = pC3->RefLo;
        pC3->RefLo   = pC3->RefHi;
        pC3->RefHi.Key      = 0;
        pC3->RefHi.pContext = NULL;

        pC2->pChild2 = pC3->pChild1;
        pC3->pChild1 = pC3->pChild2;
        pC3->pChild2 = pC3->pChild3;
        pC3->pChild3 = NULL;

        return false;
    }
    
    // If pChild1 is a 3-node, rotate its extra child over to pChild2.
    if (NULL != pC1->RefHi.pContext) {
        pC2->RefLo   = pNode->RefLo;
        pNode->RefLo = pC1->RefHi;
        pC1->RefHi.Key      = 0;
        pC1->RefHi.pContext = NULL;

        pC2->pChild2 = pC2->pChild1;
        pC2->pChild1 = pC1->pChild3;
        pC1->pChild3 = NULL;

        return false;
    }
    
    // If pChild3 exists, merge it with pChild2.
    if (NULL != pNode->RefHi.pContext) {
        pC2->RefLo = pNode->RefHi;
        pC2->RefHi = pC3->RefLo;
        pNode->RefHi.Key      = 0;
        pNode->RefHi.pContext = NULL;
        pC3->RefLo.Key        = 0;
        pC3->RefLo.pContext   = NULL;

        pC2->pChild2 = pC3->pChild1;
        pC2->pChild3 = pC3->pChild2;
        pC3->pChild1 = NULL;
        pC3->pChild2 = NULL;

        pNode->pChild3= NULL;

        Free(pC3);

        return false;
    }

    // The last resort is to merge pChild1 and pChild2.
    // This will turn pNode into a degenerate 1-node.
    pC1->RefHi = pNode->RefLo;
    pNode->RefLo.Key      = 0;
    pNode->RefLo.pContext = NULL;

    pC1->pChild3   = pC2->pChild1;
    pC2->pChild1   = NULL;
    pNode->pChild2 = NULL;

    Free(pC2);

    // Return true since pNode is degenerate and the fix-up operation
    // must propagate up to the next level of the tree.
    return true;
}


/////////////////////////////////////////////////////////////////////////////
//
//    FixThird()
//
//    This is called when pNode->pChild3 has ended up as a degenerate 1-node.
//
//    In this case, pNode is a 3-node, so we have enough values to safely
//    contain the merging.  At worst, we may delete pChild3.
//
//    Note that in this case, since merging is contained to this node, this
//    function does not need to return anything.
//
void TwoThreeInterior::FixThird(TwoThreeInterior_t *pNode)
{
    TwoThreeInterior_t *pC2 = pNode->pChild2;
    TwoThreeInterior_t *pC3 = pNode->pChild3;

    // If pChild2 is a 3-node, we need to perform a rotation.
    if (NULL != pC2->RefHi.pContext) {
        pC3->RefLo   = pNode->RefHi;
        pNode->RefHi = pC2->RefHi;
        pC2->RefHi.Key      = 0;
        pC2->RefHi.pContext = NULL;

        pC3->pChild2 = pC3->pChild1;
        pC3->pChild1 = pC2->pChild3;
        pC2->pChild3 = NULL;
    }

    // Otherwise pChild2 is a 2-node.  We have to fix pChild3 by merging it
    // with pChild2, making pNode a 2-node.
    else {
        pC2->RefHi = pNode->RefHi;
        pNode->RefHi.Key      = 0;
        pNode->RefHi.pContext = NULL;

        pC2->pChild3 = pC3->pChild1;
        pC3->pChild1 = NULL;

        pNode->pChild3 = NULL;

        Free(pC3);
    }
}

The entry point for deleting a key from the tree is Delete. This is really just a wrapper around the recursive method DeleteRec. The only work that Delete needs to do is delete the old root node if a merge operation turned the old root into a 1-node.

void TwoThreeInterior::Delete(const U32 key)
{
    if (DeleteRec(m_pRoot, key)) {

        // If a merge propagated all the way to the root, we need to delete
        // the root of the tree.
        //
        // Note that this is the only way that the depth of the tree can
        // change.  By deleting the root, the depth of every leaf node has
        // just decreased by 1.

        TwoThreeInterior_t *pTemp = m_pRoot;

        m_pRoot = m_pRoot->pChild1;

        pTemp->pChild1 = NULL;

        Free(pTemp);
    }
}

The DeleteRec does the bulk of the work for locating and deleting a key from the tree, with support from the Fix... methods and the in-order successor routines.

This code will recursively locate the node to delete (if it even exists in the tree), then remove the node. If this causes a degenerate 1-node, we need to start merging this node with one of its siblings.

If the deletion turns pNode into a 1-node, this method will return true. The caller is responsible for completing the merge (or in the case of the root, deleting the old root of the tree).

bool TwoThreeInterior::DeleteRec(TwoThreeInterior_t *pNode, const U32 key)
{
    // This is an interior node.  Determine which child should be recursed.
    // If the recursive call returned true, the node need to be merged.
    if (NULL != pNode->pChild1) {
        // Recurse down the leftmost child.
        if (key < pNode->RefLo.Key) {
            if (DeleteRec(pNode->pChild1, key)) {
                // pChild1 was turned into a 1-node.  Perform a fix-up
                // operation to turn pChild1 into a 2-node.
                return FixFirst(pNode);
            }
        }

        // The key to delete is the first key in pNode.
        else if (key == pNode->RefLo.Key) {
            VoidRef_t succ;

            // Find the smallest key that is larger than the key being
            // deleted.  This will replace the first key in pNode.
            if (InOrderSuccessor(pNode->pChild2, succ)) {
                pNode->RefLo = succ;

                // If InOrderSuccessor() returned true, the node that used
                // to contain the successor key was turned into a 1-node,
                // so we need to apply a fix-up operation to that node,
                // which in turn may cause merging operation to progress up
                // the tree.
                if (FixInOrderSuccessor(pNode->pChild2)) {
                    return FixSecond(pNode);
                }
            }
            else {
                pNode->RefLo = succ;
            }
        }

        // If pNode is a 3-node, we need to recurse down either pChild2 or
        // pChild3.
        else if (NULL != pNode->RefHi.pContext) {

            // Recurse down the second child.
            if (key < pNode->RefHi.Key) {
                if (DeleteRec(pNode->pChild2, key)) {
                    return FixSecond(pNode);
                }
            }

            // Recurse down the third child.
            else if (key > pNode->RefHi.Key) {
                if (DeleteRec(pNode->pChild3, key)) {
                    FixThird(pNode);
                    return false;
                }
            }

            // If we get here, pNode's second key is the one that needs to
            // be deleted.  That key needs to be replaced by the in-order
            // successor to the key being deleted.
            else {
                VoidRef_t succ;

                // Find the smallest key that is larger than the key being
                // deleted.  This will replace the first key in pNode.
                if (InOrderSuccessor(pNode->pChild3, succ)) {
                    pNode->RefHi = succ;

                    // If InOrderSuccessor() returned true, the node that
                    // used to contain the successor key was turned into a
                    // 1-node, so we need to apply a fix-up operation to
                    // that node, which in turn may cause merging operations
                    // to progress up the tree.
                    if (FixInOrderSuccessor(pNode->pChild3)) {
                        FixThird(pNode);
                        return false;
                    }
                }
                else {
                    pNode->RefHi = succ;
                }
            }
        }

        // Otherwise pNode is a 2-node, so the only option is to recurse
        // down the second child in search of the key to delete.
        else {
            if (DeleteRec(pNode->pChild2, key)) {
                return FixSecond(pNode);
            }
        }
    }

    // Special case for hitting a leaf node.
    else {
        // If the key to remove is the first value, we try to replace the
        // first value with the second.
        if (key == pNode->RefLo.Key) {

            // Assume there is a second key and replace the first with it.
            // If not, we have at least succeeded in NULLing out the first
            // node.
            pNode->RefLo          = pNode->RefHi;
            pNode->RefHi.Key      = 0;
            pNode->RefHi.pContext = NULL;

            // Return true if we ended up with a node that contains no keys.
            // The parent will need to handle merging the node.
            return (NULL == pNode->RefLo.pContext);
        }

        // If there is a second node, check to see if it is the key we need
        // to remove.  If so, we only need to NULL out the reference.
        // Always return false, since no merge is needed in this case.
        else if ((NULL != pNode->RefHi.pContext) &&
                 (key  == pNode->RefHi.Key))
        {
            pNode->RefHi.Key      = 0;
            pNode->RefHi.pContext = NULL;
        }
    }

    return false;
}