Performance
Performance measurements on modern computers cannot generalize to a single factor. Numerous factors can impact how well an algorithm performs, including how it is implemented, how much memory it accesses, and how much CPU work is done per memory access.
Search algorithms tend to access random memory, so unless the algorithm is being use iteratively (where it will re-access the same memory on subsequent search operations), these algorithms tend to suffer a lot of cache-line misses. This is an important factor, since modern computers tend to have CPU speeds that are much faster than main memory. Every cache-line miss forces the CPU to stall, waiting for the cache-line to load.
As such, the advantage goes to algorithms that minimize the total number of memory accesses. Traditional thinking is that CPU-intensive operations are slower. However, with modern computers, algorithms can — but not necessarily will — perform better by doing more CPU work and fewer memory accesses.
One observation about red-black trees is that they are theoretically fast due to needing less code. However, they have the bad trait of needing to touch more memory when rebalancing the tree during insertions and deletions. 2-3 trees need to access fewer nodes when inserting and deleting, but are much more complex and therefore require much more CPU load to perform.
On a system with no other loading factors, 2-3 trees gain the advantage of better performance since they require fewer unique cache-line accesses. However, on a more loaded CPU, the extra CPU cycles needed by 2-3 trees may not be available, and their performance can therefore suffer, giving red-black trees the performance advantage.
So which algorithm is going to perform better?
That is not easily answered, since there are too many factors involved, including (but not limited to) those mentioned above. The only reliable way to determine the best algorithm is to measure it in under the conditions in which it will be used.
Exterior 2-3 Trees
Advantages:
- Conceptually easy as a learning algorithm.
Disadvantages:
- More nodes are required since values are only stored in leaves.
- Very high memory usage per key.
- Extra work is needed to update cached low values when splitting/merging.
Interior 2-3 Trees
Advantages:
- Lowest average memory usage per key.
- Very good performance on systems with no other CPU load.
Disadvantages:
- More processing is required per node, since each node may store one or two keys.
Red-Black Trees
Advantages:
- Fast under both low and high CPU load.
Disadvantages:
- Nodes are smaller but more prolific since there is one node for every key in the tree.
- Rebalancing the tree requires touching more adjacent nodes to rearrange and recolor nodes, which lowers performance.
Left Leaning Red-Black Trees
Advantages:
- Based on testing, LLRBs have no advantages over standard red-black trees.
Disadvantages:
- Nodes are smaller but more prolific since there is one node for every key in the tree.
- Rebalancing the tree requires touching more adjacent nodes to rearrange and recolor nodes, which lowers performance.
- The left leaning requirement requires even more work to rebalance the tree than a basic red-black tree.
Memory Usage
For purposes of memory usage, I will assume a 32-bit processor, with no packing. Additionally, I include the extra heap memory that is associated with each allocated buffer. Since this varies between compilers, platforms, and even release versus debug builds, I will assume an average of 16 bytes per allocation (but it can be much higher).
External 2-3 trees require each key to be stored in a node by itself. This requires n nodes simply to store the leaves of the tree. On top of this, there need to be enough internal nodes to populate the tree, which requires on average 2/3 as many internal nodes as there are leaves (assuming half of internal nodes are 2-nodes and half are 3-nodes).
Each node contains nine 32-bit words, plus 16 bytes of heap. Since the average number of nodes in the tree is 5/3 the number of keys, the average memory usage is 86.6 bytes per key.
Internal 2-3 trees allow keys to be stored in internal nodes. Assuming that an average of 1.5 keys are stored in each node, the total number of nodes is 2/3 the number of keys.
Each node contains seven 32-bit words, plus 16 bytes of heap. Since the average number of nodes in the tree is 2/3 the number of keys, the average memory usage is 29.3 bytes per key.
Red-black trees are binary trees, so there needs to be one node for every key in the tree.
Each node contains five 32-bit words, plus 16 bytes of heap. Since the number of nodes in the tree is the same as the number of keys, the average memory usage is 36 bytes per key.
Since left leaning red-black trees are identical in storage to basic red-black trees, the average memory usage is also 36 bytes.
The following table shows the average memory required per key for each of the algorithms examined:
| Algorithm | Bytes Per Key |
|---|---|
| External 2-3 | 87 |
| Internal 2-3 | 29 |
| Red-Black | 36 |
| LLRB | 36 |
Internal 2-3 trees have the lowest average memory usage. Total memory usage is not the sole factor of performance, but the less memory an algorithm needs to access, the better it will perform on systems with slow main memory.
Due to limits on specific embedded processors used for this testing, any performance generalization is not reliable. If you need to use balanced trees on an embedded processor (or any other processor that has the CPU and memory running at similar clock speeds), the different algorithms should be tested on that hardware to determine which one yields the best performance.
To avoid non-disclosure issues, the performance results from certain embedded processors are not presented here.
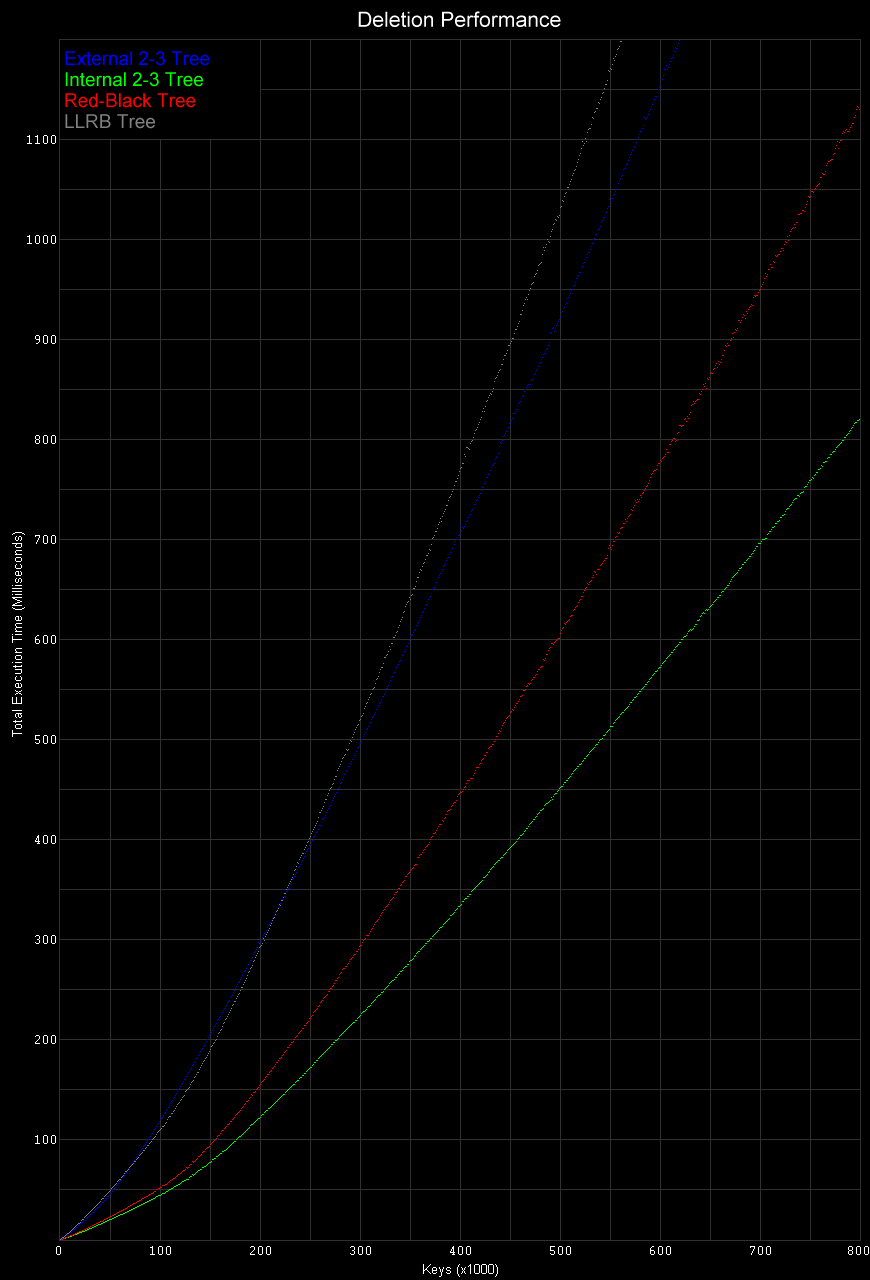
Look-Up Performance
All of the following performance measurements were taked on a Core 2 Duo 6600 (2.4 GHz). Similar results were obtained on several other variations of Core 2 processors.
From the following table, it is clear that except for exterior 2-3 trees, all of the algorithms studied have virtually identical performance on look-up operations.
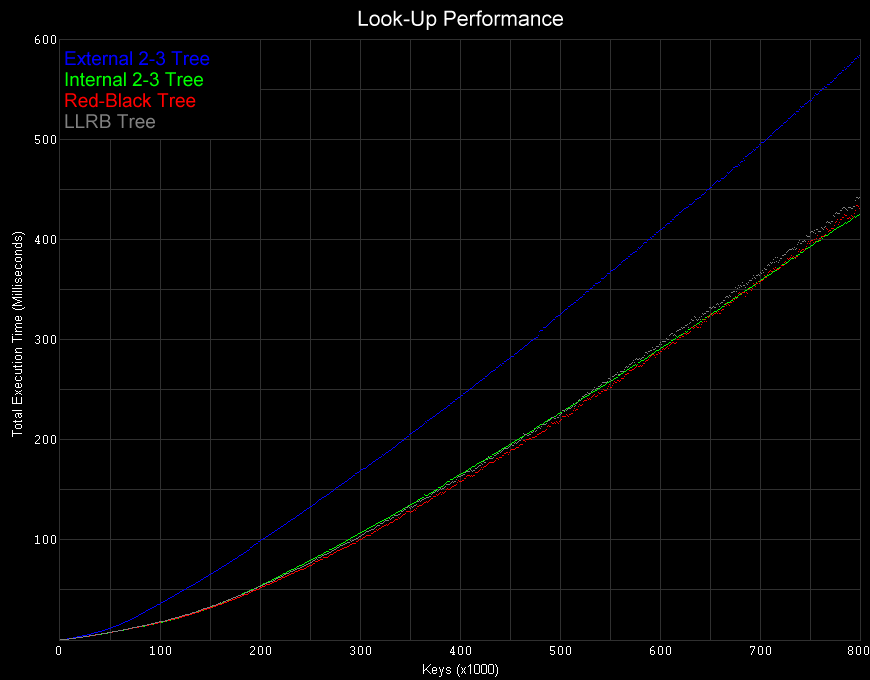
Insertion Performance
When inserting new values into the tree, internal 2-3 trees and basic red-black trees yield the best performance. For sufficiently large numbers of keys (over 200,000), 2-3 trees consistently provide the best performance.
On the other hand, the performance of LLRBs is surprisingly bad, approximately as bad as external 2-3 trees. One can only assume this poor performance is due to the additional node rearrangement required to adhere to the left-leaning requirement.
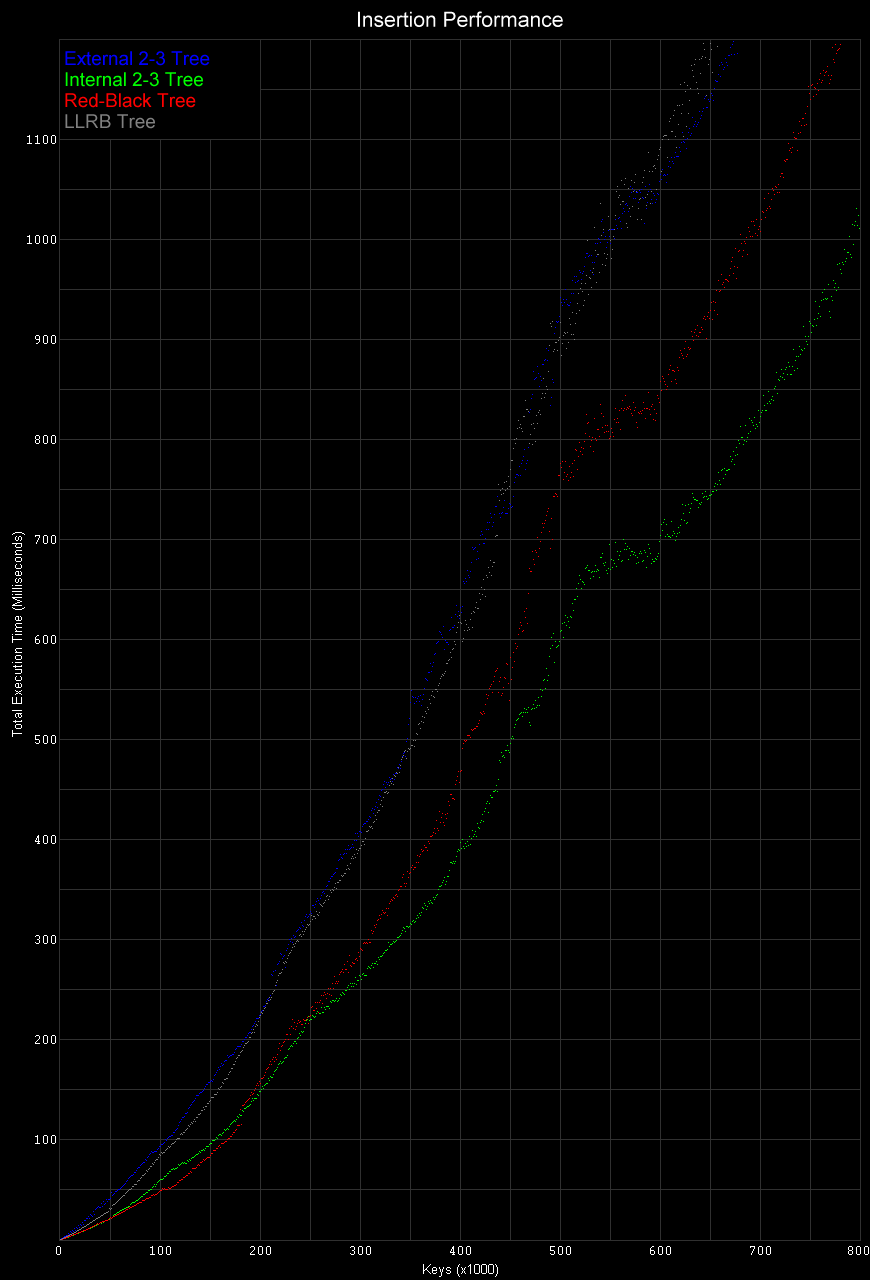
Deletion Performance
Internal 2-3 trees yield the best performance when deleting keys. Unlike the other algorithms, internal 2-3 trees only need to delete memory half of the time. By needing to touch fewer nodes when rearranging data, and by not actually needing to free memory for every deletion, this algorithm has very good performance.